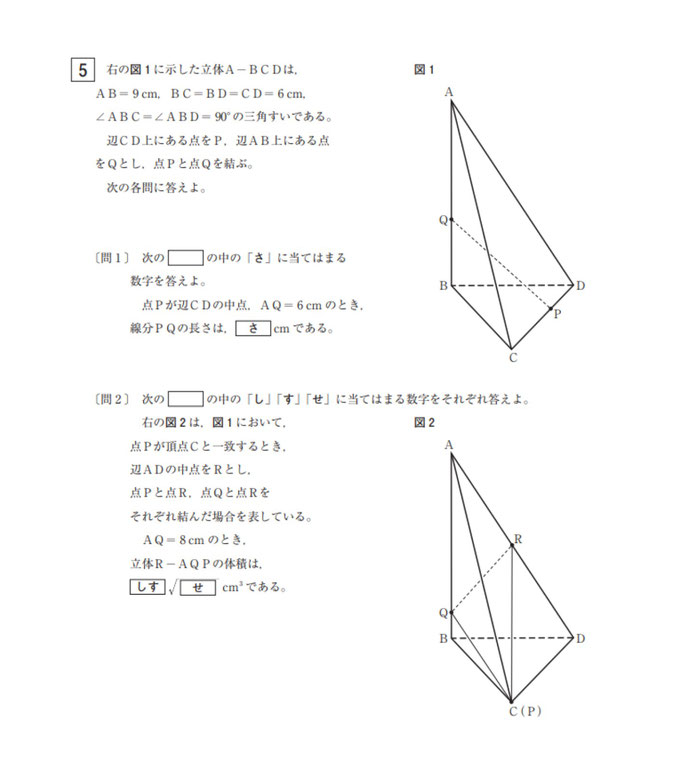
さて、(問1)です。
点Qと頂点Cと頂点Dを結ぶと切断断面図の三角形バージョンができます。上から見ると、底辺は正三角形なので、点Pが中点ならば二等辺三角形になります。
断面図三角形(QCD)の底辺(CD)は6cmで問題ありませんが、QCとQD(2つとも同じ)の長さですね。
横から三角形ABCを見ると、BQが3cm、ということは3cm、6cmと斜辺xcmの直角三角形を三平方の定理で導きます。
3の2乗+6の2乗=xの2乗
これを解いて、x=3√5
次は、切断三角形QCDを半分に切ります。QPですね。
すると、角CPQは直角なので、直角三角形の出来上がり。また、三平方の定理登場。
QPをyとして、3√5の2乗+3の2乗=yの2乗
これをyについて解くと、+-6 よって6cmが正解
(問2)
さあ、最難題です。頭の中で図形をいろいろ回したり、、、そのうち、わけわかめになります。。。
ひとまず、裏紙で作ってみました。
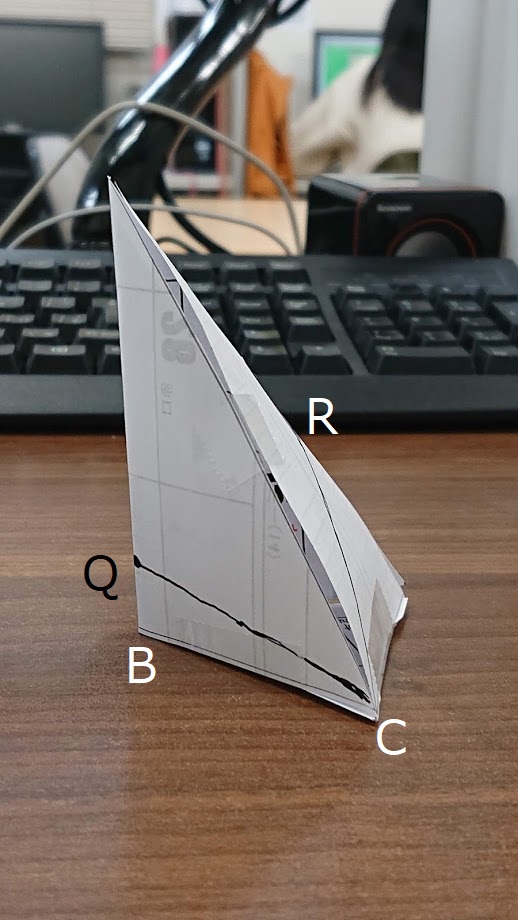
問題に書いてある向きですとこんな感じ。↑↑
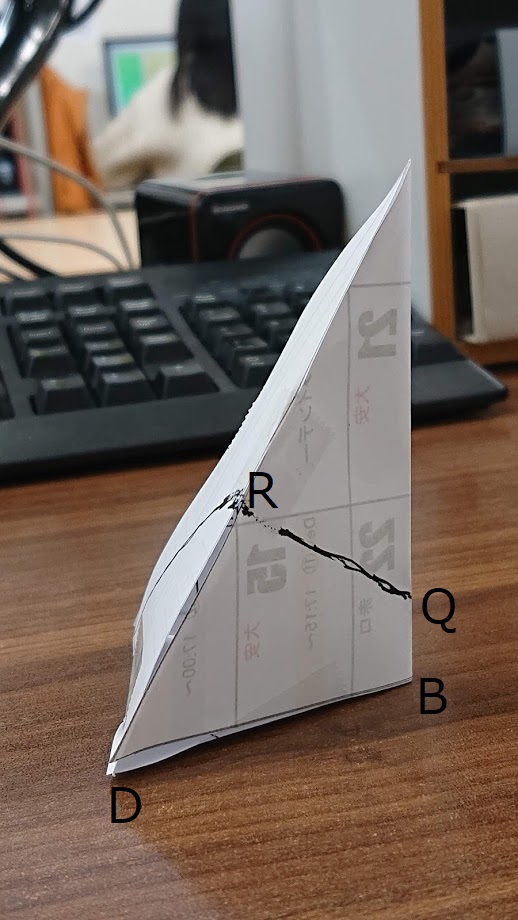
↑ 立てた状態で反対側から見た感じ

で、底辺を面ABCにして斜め上から撮りました。
頂点Aを左にして横にすると、2等辺三角形(面ACD)を見るため、点Rの高さが図れません。うーん、と思い、紙で立体を作成して反対向き(上記図)にしたら「おー!」となりました。
面BDAは直角三角形ですので、ここで中点連結定理が使えます。
ただ、この面をそのまま使ってはいけません。
高さは頂点Dから辺BCの中点に下ろした線になります。まずはこの長さを出します。(Zとします)
3の2乗+Zの2乗=6の2乗
これを解いて、Z=3√3
で、点RはADの中点なので、その半分。3√3/2となります。これで、三角錐の高さが出ました。
あとは、底辺(三角形AQP)を求めます。これは簡単なので、解説省略。
計算すると、底辺は24
よって、24×2分の3√3×1/3(推だから)=12√3
めでたしめでたし

