
(問1)
平行四辺形であれば、同位角、錯覚が使えますね。
まず、角ADCは対角の角ABCと同じ50°です。
三角形APDで見たときに、角APCは角APDの外角です。よって、
角APC=角DAP+角ADP となります。
なので、(a+50)度 (イ)が正解。
(問2)①
証明問題ですが、模範解答にありますので省略します。
ポイントは、2組の角がそれぞれ等しい、という相似条件を導くことです。
(問2)②
一見、「はぁ?」という問題ですね。三角形を対比して面積比で導く問題は多々ありますが、ただの四角形では、どうやって・・・??と、少し考えました。。。
しかし、やはり相似な三角形と相似比で求められる問題には変わりません。
まず、説明がややこしくなるので、以下の通りとしますね。
三角形AQRを「X」、三角形ABPを「Y」とします。
で、大事なことは補助線を引くことです。
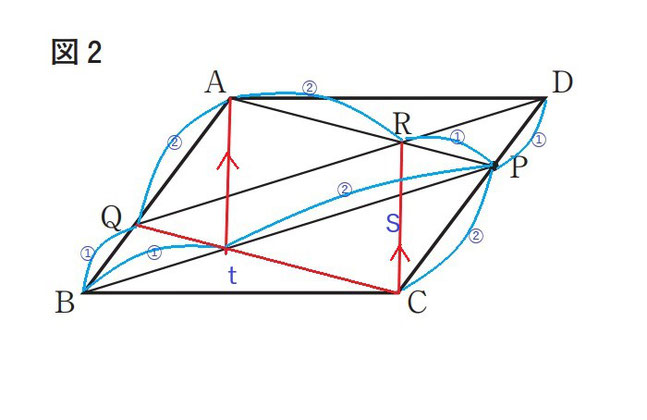
頂点Aから線RCと平行な線を引き、線BPとの交点を点tとします。
それで、それぞれの線分比を①と②で書きました。
解き方のポイントは、問われているものを見て、三角形AQRの何倍?とあるので、基準を三角形AQR(X)とすることです。
では、いきます。
面積比 X:Y=4:9 Y=9/4X …①
三角形AtP=Y(9/4X)×2/3 =3/2A
※Bt:Ptが①:②なので面積比も1:2になります。
三角形RSP=3/2A×1/9=1/6A …②
※1/9は面積比です。
X:Y=4:9なので、四角形QBPR:Y=5:9 5Y=QBPR×9 QBPR=5/9Y
四角形QBPR=5/9YのYに①を代入。
9/4X×5/9=5/4X …③
さあ、ラストです。
四角形QBPR-三角形RSP=③-②
5/4X-1/6X=13/12X
よって、答えは13/12
です。
めでたし。

