
2次方程式 x2+5x-3=0
まず、因数分解公式が使えるか、さっと確認。
掛け算して-3、加減で5になる組み合わせは、えーっと、ないなぁ。
すると、解の公式を使うことになります。
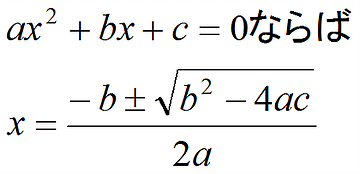
しかし、これってあまり好きではない。いかにも公式に当てはめるだけという数学っぽくないのである。せっかくなので、高校数1で習う「平方完成」で解いちゃいましょう。これは実は3年の因数分解でも出てくる解き方です。
x2+5x-3=0
x2+5x に何かをたして(A+B)2 の形にします。
真ん中の5を半分にした数字の2乗が右(B)に来るので、
(x+5/2)2 とします。確認のため、これを展開すると、
x2+5x+25/4 となります。余分な数字が25/4なので、同じ数を引いてしまいます。
(x+5/2)2-25/4 で、もとの-3=0を付けたして、
(x+5/2)2-25/4-3=0
-25/4-3を計算。-25/4-12/4なので、-37/4
これを右辺に移動。
(x+5/2)2=37/4
両辺を平方して、 x+5/2=±√37/4
x+5/2=±√37/2
-5±√37
x=—————
2
2分の、マイナス5プラスマイナスルート37 ・・・答え
どうですか。この方が解いたという気になれませんか??え、余計面倒?
そんなことはありません。この解き方は「平方完成」という高校の2次関数で出てきます。
今のうちに慣れておくといいですよー。

